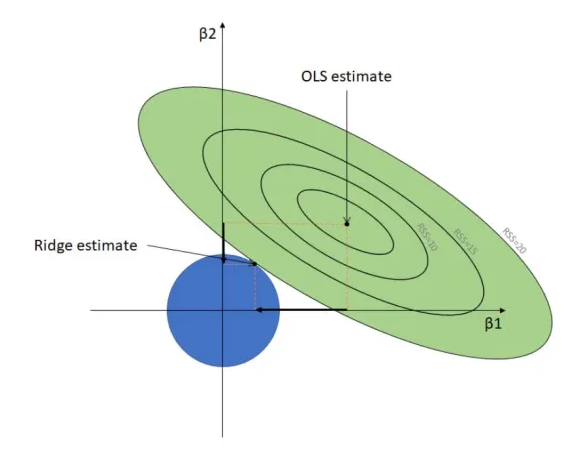
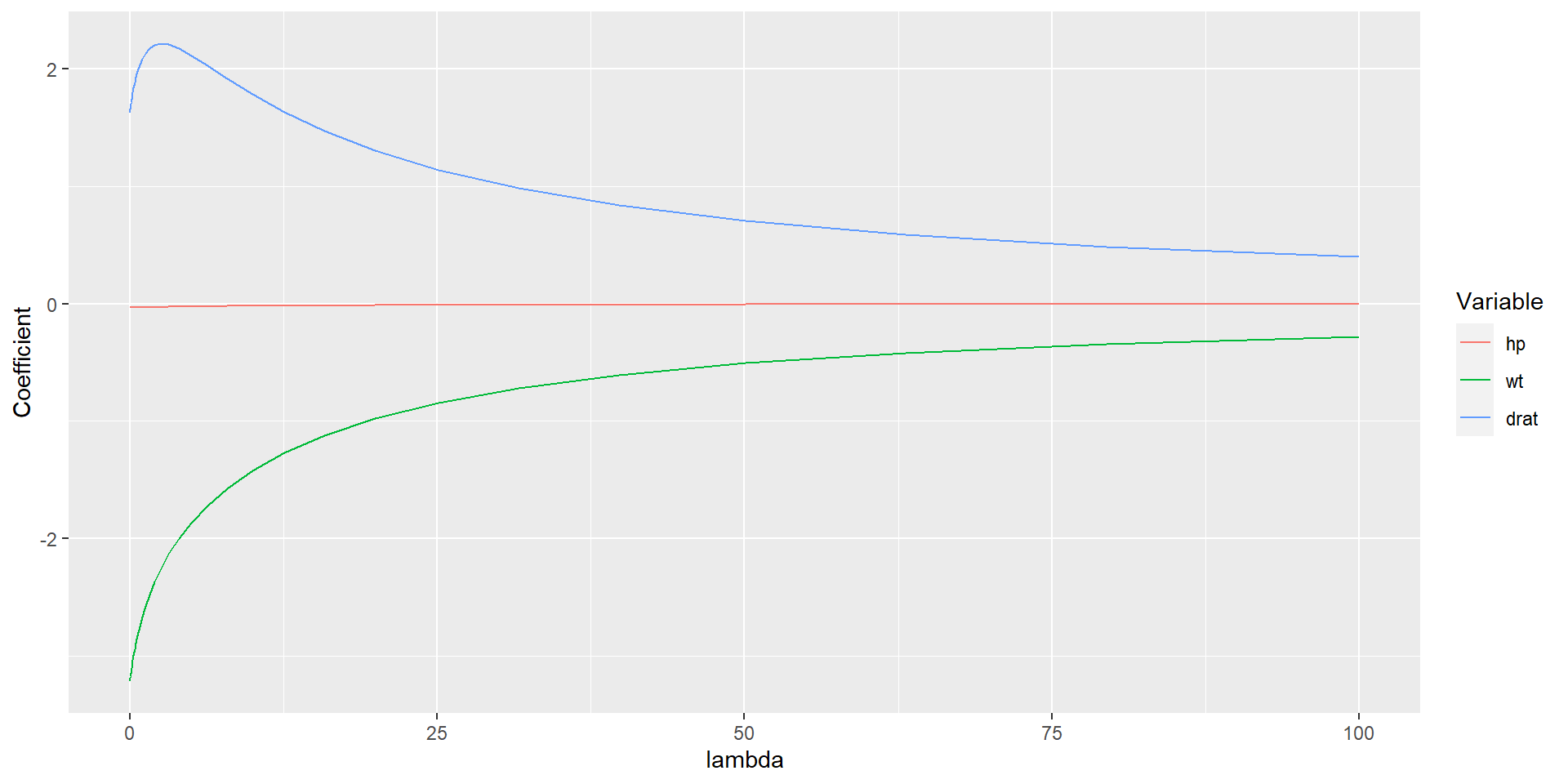
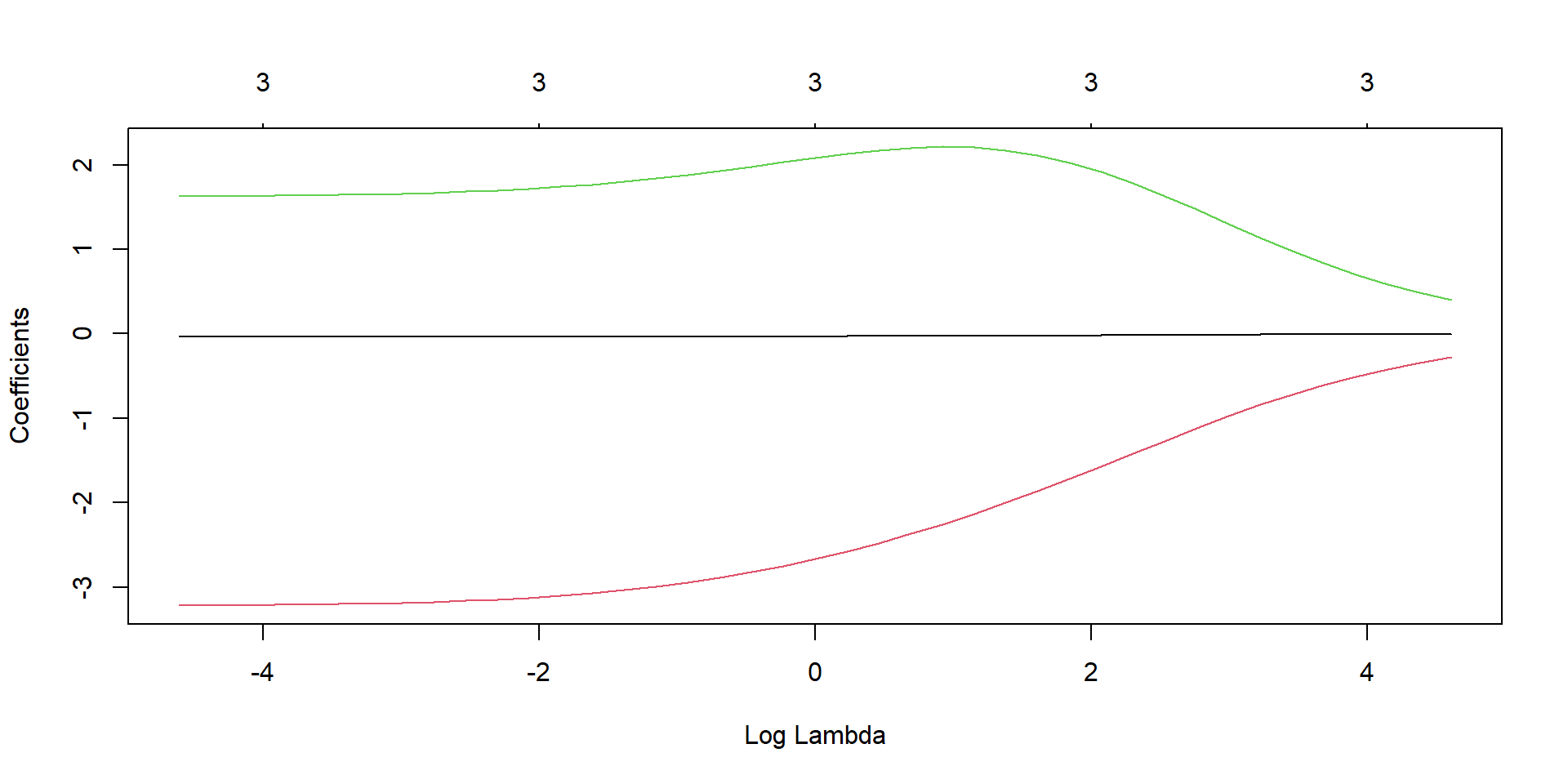
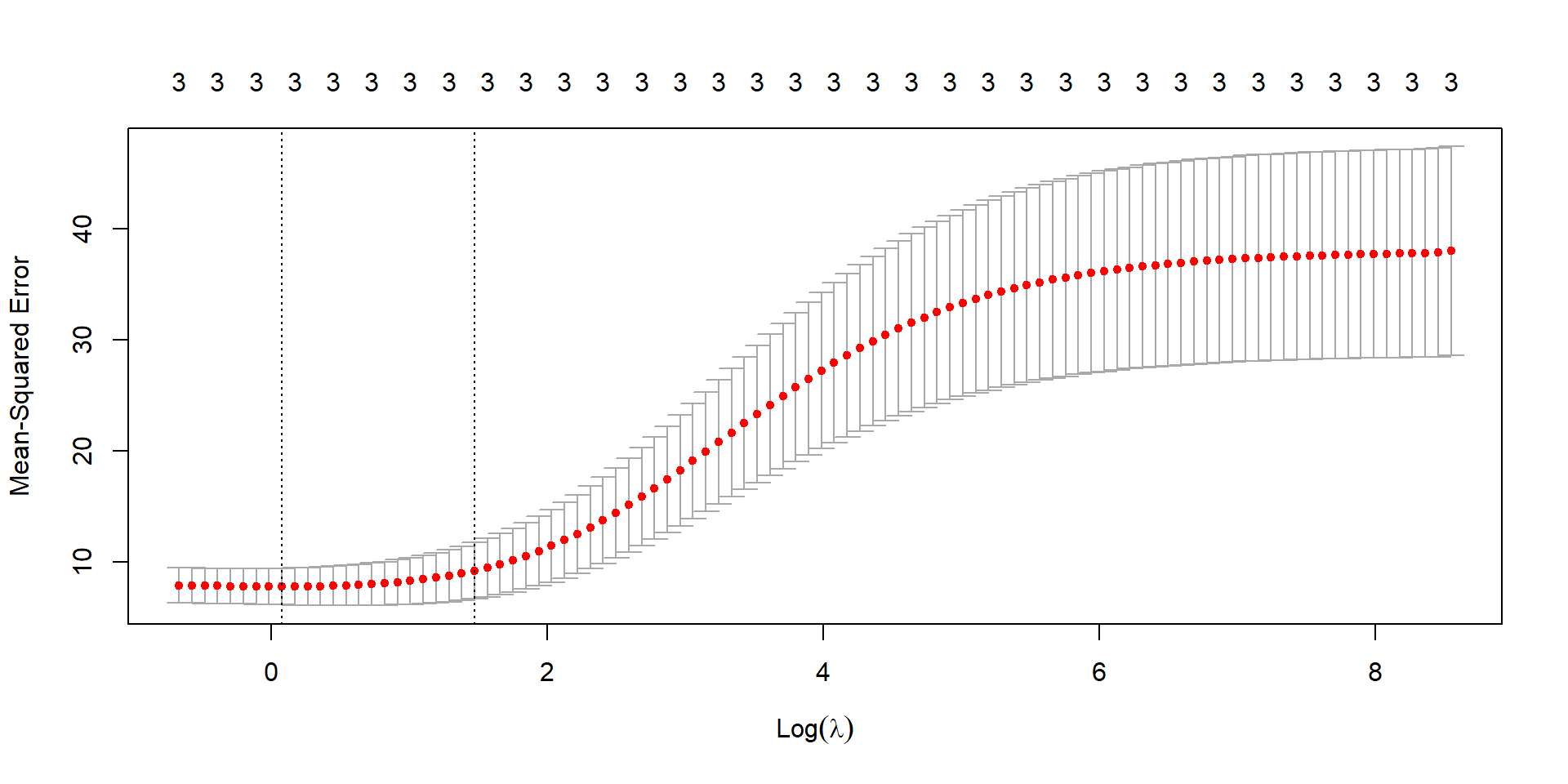
library(glmnet)
x_var <- data.matrix(mtcars[, c("hp", "wt", "drat")])
y_var <- mtcars[, "mpg"]
lambda_seq <- 10^seq(2, -2, by = -.1)
fit <- glmnet(x_var, y_var, alpha = 0, lambda = lambda_seq)
summary(fit) Length Class Mode
a0 41 -none- numeric
beta 123 dgCMatrix S4
df 41 -none- numeric
dim 2 -none- numeric
lambda 41 -none- numeric
dev.ratio 41 -none- numeric
nulldev 1 -none- numeric
npasses 1 -none- numeric
jerr 1 -none- numeric
offset 1 -none- logical
call 5 -none- call
nobs 1 -none- numeric